题目链接：

pid=1133

【题意】

电影票50块一张

有m个人手里正好有50块，n个人手里正好有100块，售票厅開始没有钱。问，有多少种排队的方式，能够让每一个人都买上票。

（假设售票厅没有50块零钱，则持有100块的人买不了票）

【分析】

显然。当m<n的时候，有0种排列方式。

当m>=n的时候：

用0。代表手里仅仅有50块的人，1，代表手里仅仅有100块的。

则0110100 这样的情况不能满足条件（到第三个人就买不了）

我们把包含第三个人及他之前的人 翻转 （1->0，  0->1）

1000100 出现了这个序列； 

0110100   有 4个0,3个1    1000100  有5个0 ，2个1

每个不能满足的情况都相应这样一个序列 所以 不能满足的条件的情况共同拥有

C（m+1,m+n）；

我们计算公式就是：合法的排列方式=全部排列方式-非法排列方式

于是就有了F（N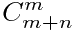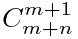）=(-)*m！*n！  ；

然后再化简一下;

F(N) =（m+n）！

*（m-n+1）/（m+1）。

由于数据过大，所以用了JAVA大数来解决

【代码】

import java.util.*;import java.math.BigInteger;public class Main{    public static void main(String[] args){            int a,b;            Scanner in=new Scanner(System.in);            int cnt=0;            while(in.hasNext()){                cnt++;                a=in.nextInt();                b=in.nextInt();                BigInteger ans=BigInteger.ONE;                if(a==0&&b==0)break;                if(a